There are some good discussions on the Fast.ai forums here and lesson notes that talk about label smoothing. It showed up in Lesson 12 video along with Mixup.

Label smoothing helps your model not become too confident by penalizing very high probability outputs from the model. In turn, you will robust to potentially mis-labeled cases in the data. I dove into this more when writing up my results for the HAHA 2019 Compeition. I was inspired by the forum post to generate my own snippet to see the difference between the BCE and the label smoothing losses.

import numpy as np
import matplotlib.pyplot as plt

probs = np.linspace(0.5,0.99)
eps = 0.1
soft_out = (1-eps) * -np.log(probs) + eps/2. * -np.log(1-probs)
plt.plot(probs,soft_out, label="Label Smoothing CE")
plt.plot(probs, -np.log(probs), label="Cross Entropy")
plt.xlabel("prob")
plt.legend()
_ = plt.ylabel("Smoothed CE")

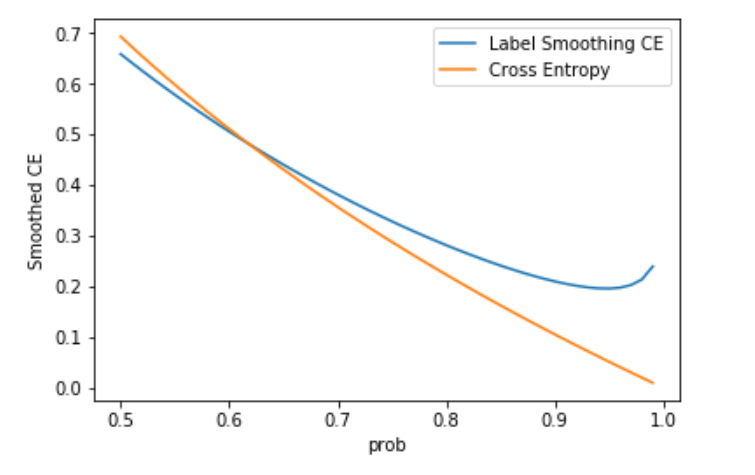
This graph shows the difference between the usual Binary Cross Entropy (BCE) and the label smoothed values for predicted probabilities >0.5. When <0.5, they are about the same. Looking at the graph, I noticed two things:

1. The minimum comes at 0.95 - if you have predictions higher than that, they are penalized.
2. Even at 0.95, the loss is non-zero.

With BCE, you get losses that are smaller and smaller (and produce smaller gradients) as your prediction approaches 1. This is a model becoming overconfident and the original paper (section 7) talks about this exact case. The loss here shows that this is discourage and loss will be minimized when you predict at 0.95.

In my own experiments, I have found that this is a strong enough regularizer that you can skip the gradual unfreezing in an NLP classifier and train directly without catastrophic forgetting of the prior weights in the model.